Instructions for optimization with PSG Run-File, PSG MATLAB Toolbox, PSG MATLAB Subroutines and PSG R.

PROBLEM 1: problem_MaxRet_Prob
Maximize Linear (maximizing estimated return)
subject to
Pr_pen ≤ Const1 (probability constraint)
Linear = 1 (budget constraint)
Box constraints (upper bounds on positions)
——————————————————————–
Pr_pen = Probability Exceeding Penalty for Loss
Box constraints = constraints on individual decision variables
——————————————————————–
Data and solution in Run-File Environment

Problem Datasets				# of Variables	# of Scenarios	Objective Value	Solving Time, PC 2.66GHz (sec)
Dataset1	Problem Statement	Data	Solution	10	1,000	0.00120185276974	0.01

——————————————————————–
Data and solution in MATLAB Environment

Problem Datasets				# of Variables	# of Scenarios	Objective Value	Solving Time, PC 2.66GHz (sec)
Dataset1	Matlab code	Data	Solution	10	1,000	0.00120185	0.02

——————————————————————–
Data and solution in R Environment

Problem Datasets				# of Variables	# of Scenarios	Objective Value	Solving Time, PC 2.66GHz (sec)
Dataset1	R code	Data		10	1,000	0.00120185	0.02

PROBLEM 2: problem_MaxRet_VaR
Maximize Linear (maximizing estimated return)
subject to
Var_risk ≤ Const2 (VaR constraint)
Linear = 1 (budget constraint)
Box constraints (upper bounds on positions)
——————————————————————–
Var_risk = VaR Risk for Los
Box constraints = constraints on individual decision variables
——————————————————————–
Data and solution in Run-File Environment

Problem Datasets				# of Variables	# of Scenarios	Objective Value	Solving Time, PC 2.66GHz (sec)
Dataset1	Problem Statement	Data	Solution	10	1,000	0.00120185276974	0.01

——————————————————————–
Data and solution in MATLAB Environment

Problem Datasets				# of Variables	# of Scenarios	Objective Value	Solving Time, PC 3.50GHz (sec)
Dataset1	Matlab code	Data	Solution	10	1,000	0.00120185	0.01

——————————————————————–
Data and solution in R Environment

Problem Datasets				# of Variables	# of Scenarios	Objective Value	Solving Time, PC 3.50GHz (sec)
Dataset1	R code	Data		10	1,000	0.00120185	0.01

CASE STUDY SUMMARY
This case study demonstrates the equivalence between chance constraints and VaR constraints, as explained in Sarykalin et al. (2008). Several engineering applications deal with probabilistic constraints such as the reliability of a system or a delivery system likelihood to meet a demand. In portfolio management, often it is required that portfolio loss with high reliability should not exceed some value. In these cases an optimization model can be set up so that constraints are required to be satisfied with some probability level rather than almost surely. Chance constraints and VaR (percentile) constraints are closely related. We will illustrate numerically the equivalence of the constraints:
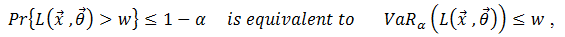, i.e., the constraint assuring that the probability that loss 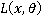exceeding w is less or equal than 1- 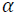is equivalent to the constraint that VaR (percentile) with confidence level 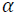is less or equal than w.
We solve two portfolio optimization problems. In both cases we maximize the estimated return of the portfolio. In the first problem, we impose a constraint on probability; in the second problem, we impose an equivalent constraint on VaR. We expect to obtain at optimality the same objective function value and similar optimal portfolios for the two problems.

References
• Sarykalin, S., Serraino, G., and Uryasev, S. (2008): VaR vs CVaR in Risk Management and Optimization, INFORMS Tutorials in Operations Research, Institute for Operations Research and the Management Sciences, Hanover, MD, 270–94.
• Rockafellar, R.T. (2007): Coherent Approaches to Risk in Optimization Under Uncertainty, INFORMS Tutorials in Operations Research. Institute for Operations Research and the Management Sciences, Hanover, MD, 38–61.